Solving multi-step equations involves using algebraic properties to isolate variables. These equations require distributing terms‚ combining like terms‚ and applying inverse operations. Mastering this skill is essential for advancing in algebra and real-world problem-solving.
Step-by-Step Guide to Solving Multi-Step Equations
Start by distributing terms and combining like terms. Use inverse operations to isolate the variable‚ ensuring each step is clear and logically follows the previous one.
Distributing Terms and Combining Like Terms
First‚ apply the distributive property to expand any expressions with parentheses. For example‚ in the equation 5(x ⎯ 2) ⎯ 10x = 55‚ distribute the 5 to get 5x ⎯ 10 ⎯ 10x = 55. Next‚ combine like terms by adding or subtracting coefficients of the same variable. Here‚ 5x ⎯ 10x results in -5x‚ simplifying the equation to -5x ⎯ 10 = 55. This step is crucial for simplifying the equation before isolating the variable.
Isolating the Variable
After simplifying the equation by distributing and combining like terms‚ the next step is to isolate the variable. This involves using inverse operations to move all constant terms to the opposite side of the equation. For example‚ in the equation -5x ⎯ 10 = 55‚ add 10 to both sides to get -5x = 65. Then‚ divide both sides by -5 to solve for x‚ resulting in x = -13. Always perform the same operation on both sides to maintain equality. If the variable is multiplied or divided by a coefficient‚ use the inverse operation to solve for it. This step ensures the variable stands alone‚ allowing you to find its value accurately. Checking the solution by substituting it back into the original equation confirms its validity. Isolating the variable is the final step in solving multi-step equations and requires careful application of algebraic properties.
Special Cases in Multi-Step Equations
Special cases in multi-step equations require careful analysis. These include equations with no solution‚ infinite solutions‚ or variables on both sides. Identifying these scenarios ensures accurate problem-solving.
Equations with Variables on Each Side
Equations with variables on both sides require careful manipulation to isolate the variable. Start by subtracting the same term from both sides to gather variables on one side. For example‚ in the equation 2x + 5 = 3x ⏤ 2‚ subtract 2x from both sides to get 5 = x ⎯ 2. Then‚ add 2 to both sides to find x = 7. Always use the Addition or Subtraction Property of Equality to maintain balance. If coefficients differ‚ divide both sides by the coefficient after isolating the variable. This method ensures accuracy and clarity in solving such equations.
No Solution or Infinite Solutions
Some multi-step equations may result in no solution or infinite solutions. No solution occurs when simplifying leads to a contradiction‚ like 0 = 5. Infinite solutions arise when the equation simplifies to a true statement‚ like 0 = 0‚ meaning any value satisfies it. To identify these cases‚ simplify the equation fully. If variables cancel out and you’re left with a false statement‚ there’s no solution. If you end up with a true statement‚ there are infinite solutions. Always check your work to ensure accuracy and interpret the results correctly for proper problem-solving.

Real-World Applications of Multi-Step Equations
Multi-step equations are vital in real-world scenarios‚ enabling problem-solving in various fields. In finance‚ they help calculate interest rates or investment returns. In physics‚ they model motion‚ combining speed‚ time‚ and acceleration. Engineers use them to design structures‚ while biologists apply them to population growth models. These equations are essential for budgeting‚ mixing solutions‚ and even cooking. Solving them accurately ensures practical success‚ making them a cornerstone of STEM disciplines and everyday decision-making.
Checking Solutions for Accuracy
Verifying solutions ensures the correctness of multi-step equations. Substitute the found value back into the original equation. Simplify both sides to confirm equality. If both sides match‚ the solution is accurate. This step prevents errors from invalidating results‚ reinforcing understanding and confidence in problem-solving.

Common Mistakes to Avoid
Common mistakes include forgetting to distribute terms properly‚ misapplying inverse operations‚ or combining like terms incorrectly. Students often overlook signs when multiplying or dividing‚ leading to incorrect solutions. Additionally‚ rushing through steps can result in errors. It’s crucial to work methodically and double-check each operation to maintain accuracy and ensure the correct isolation of the variable.
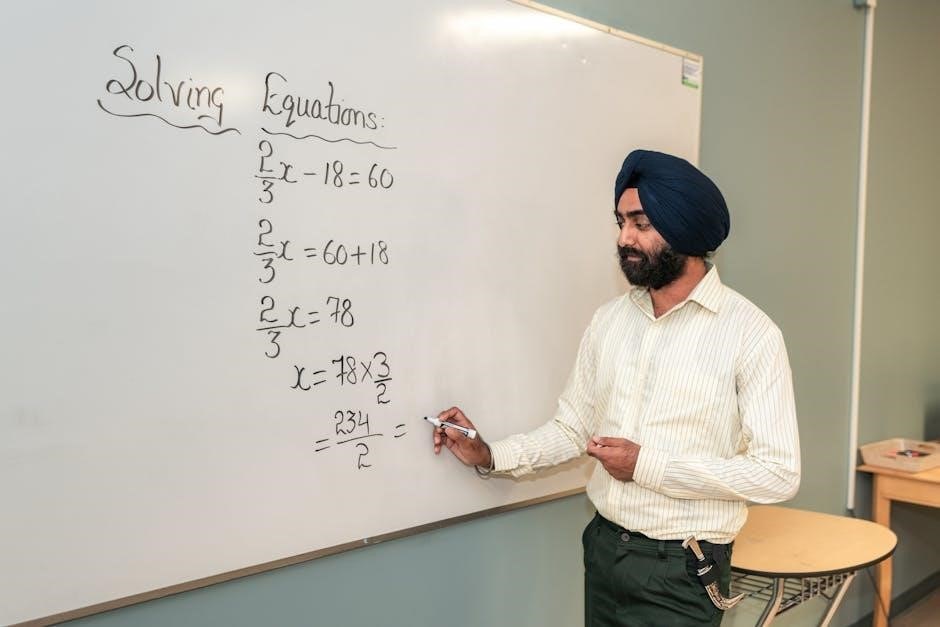
Practice Resources for Mastery
Utilize worksheets and online tools like Kuta Software for targeted practice. Guided exercises and answer keys help reinforce concepts and ensure accuracy in solving multi-step equations.
Worksheets and Exercises
Worksheets and exercises are essential tools for mastering multi-step equations. Downloadable PDF resources‚ such as those from Kuta Software‚ provide structured practice with detailed examples. These exercises often include step-by-step guides‚ starting with basic problems like 5(x ⏤ 2) ⏤ 10x = 55 and progressing to more complex scenarios. Worksheets typically cover distributing terms‚ combining like terms‚ and isolating variables‚ ensuring a comprehensive understanding. Many resources include answer keys‚ allowing students to check their work and identify areas for improvement. Additionally‚ exercises often focus on specific skills‚ such as solving equations with variables on both sides or identifying cases with no solution or infinite solutions. Regular practice with these materials helps build problem-solving confidence and reinforces algebraic concepts. For advanced learners‚ worksheets may incorporate real-world applications‚ making the practice more engaging and relevant. Consistent practice with these exercises is key to achieving proficiency in solving multi-step equations.
Online Resources and Tools
Online resources and tools offer versatile ways to learn and practice solving multi-step equations. Websites like Docsity provide comprehensive guides and downloadable PDFs‚ such as the “Six-Step Problem Solving Process‚” which detail methods for tackling complex equations. Additionally‚ platforms like Kuta Software offer interactive worksheets that cater to different skill levels. These tools often include step-by-step solutions and answer keys‚ enabling self-assessment. For advanced learners‚ resources like “Solving Multi-Step Equations Worksheets” from Download Paradise extend practice into real-world applications. Online forums and educational websites also share tips and strategies‚ such as using algebraic properties of equality and inverse operations. These resources are invaluable for students seeking to master multi-step equations‚ offering both structured practice and innovative problem-solving techniques. Utilizing these tools can significantly enhance understanding and proficiency in algebraic problem-solving.

Advanced Strategies for Complex Equations
Advanced strategies involve applying algebraic properties‚ using inverse operations‚ and combining like terms effectively to isolate variables and solve real-world problems efficiently.
Using Algebraic Properties
Algebraic properties are fundamental tools for solving multi-step equations. The distributive property allows you to expand expressions like ( a(b + c) = ab + ac )‚ simplifying equations. Combining like terms (e.g.‚ ( 3x + 2x = 5x )) reduces complexity. Inverse operations‚ such as addition and subtraction or multiplication and division‚ help isolate variables. For example‚ to solve ( 2x + 3 = 7 )‚ subtract 3 from both sides‚ then divide by 2. These strategies ensure accuracy and efficiency in solving complex equations. By applying these properties systematically‚ you can break down multi-step problems into manageable parts‚ leading to clear solutions. Mastering algebraic properties is essential for advanced problem-solving in mathematics and real-world applications.
Mastering multi-step equations is a cornerstone of algebraic proficiency; By systematically applying algebraic properties‚ distributing terms‚ and isolating variables‚ you can confidently solve complex problems. Always double-check your work to ensure accuracy; Start by simplifying expressions‚ then use inverse operations to solve for the variable. Regular practice and reviewing common mistakes will solidify your understanding. For challenging equations‚ break them into smaller‚ manageable steps. Real-world applications make these skills invaluable for problem-solving. Lastly‚ leverage online resources and practice worksheets to reinforce your learning. With persistence and attention to detail‚ you’ll become proficient in solving multi-step equations and unlock advanced mathematical concepts.






